Introduction

Humans are capable of a high level of abstraction when thinking about, recognizing and describing objects to other. In this work, our goals is to replicate similar abilities with a neural network that is able to represent an object by decomposing it into parts such that another neural agent can recognize it with as few parts as possible using an interpretable communication protocol.

To this end, we propose Primitive-based Sketch Abstraction as a new representation learning task, where the goal is to represent free-form drawings, i.e. sketches, by means of a fixed set of simple primitives. Sketches are an excellent tool for this task as they capture the essential parts of an object and humans have varying drawing styles and skills, causing different participants to draw the same instance of a real object in different ways. This observation makes finding common shapes and patterns for object categories an interesting task to better understand how humans think about concepts and what primitives they use to express them.

To solve the Primitive-based Sketch Abstraction task, we propose a self-supervised deep model, i.e. Primitive-Matching Network (PMN), to learn interpretable abstractions of a given object illustration without requiring any ground-truth abstraction. Our PMN model exposes interpretable insights about the data, making it much easier to compare and contrast sketches, e.g. a human face is composed of a big circle for the head, two small lines for the eyes and one arc for the mouth whereas a cat face is similar to a human face but has triangles on top of the head for its ears.

Primitive-Matching Network (PMN)

Our PMN model replaces each stroke of a sketch with a single drawing primitive. This is achieved by mapping each stroke to its most similar primitive in a given set, and predicting an affine transformation that aligns the selected primitive to the target stroke. We train PMN by comparing the distance-transform of target strokes and their primitive-based version. At test time, given a sketch, we can efficiently choose a set of primitives and their spatial transformations, such that the generated sketch is fully composed of primitive shapes while being as similar as possible to the original one.

The following model figure describes the pipeline PMN in more detail.

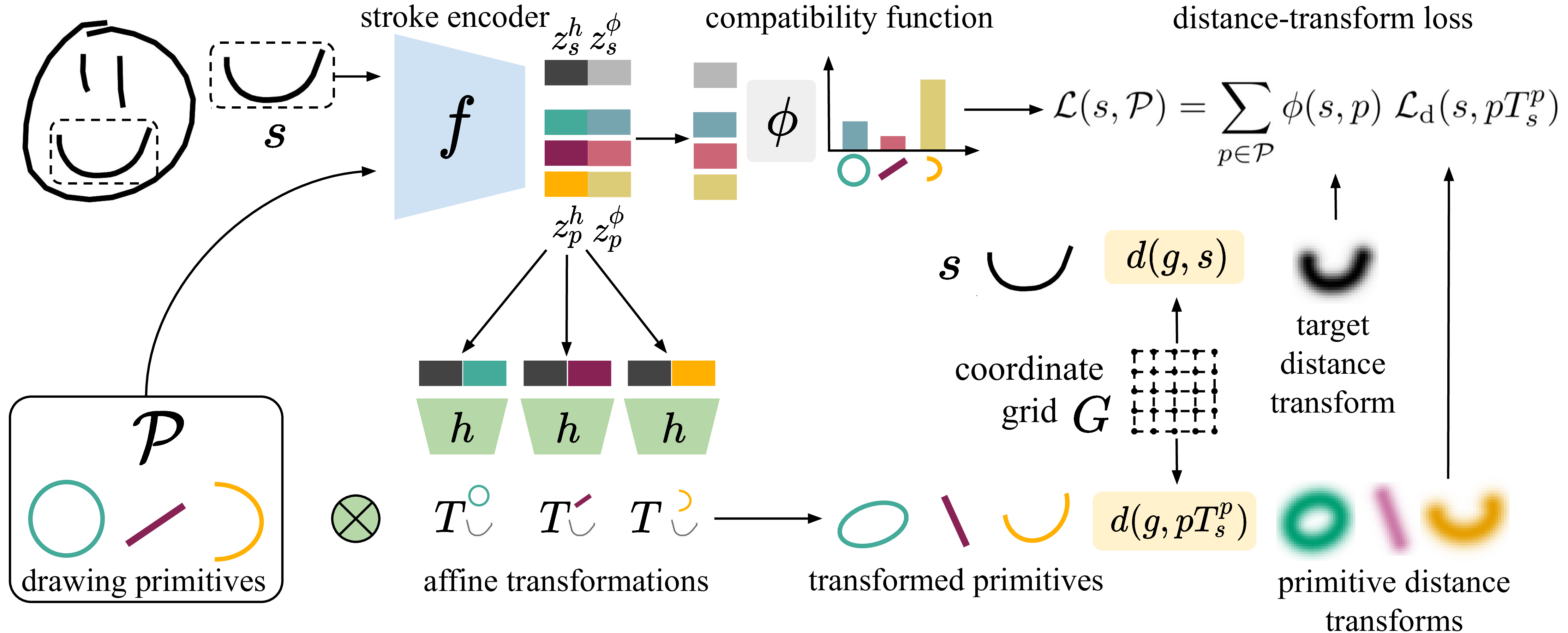
A human-drawn sketch $\mathbf{s}$ is composed of a set of strokes (i.e. $\mathbf{s}=\{s_1,\dots,s_n\}$) and each stroke is defined as a sequence of two-dimensional points of length $m(s_i)$. Additionally, we have a set $\mathcal{P}$ of drawing primitives that we want to use to represent our sketches, where each primitive is also a sequence of points. Since we want to re-draw each stroke $s\in\mathbf{s}$ with a primitive $p\in \mathcal{P}$, we need to first map each stroke ${s}_i$ to its closest primitive ${p}_i\in \mathcal{P}$, and second we need to compute the affine transform parameters making the primitive ${p}_i$ better fit the original stroke $s_i$.

To transform the primitives in such a way that they better match a given target stroke, we instantiate two functions, a stroke encoder $f:\mathcal{S}\rightarrow \mathbb{R}^d$, mapping a stroke (or primitive) to a d-dimensional embedding, and an alignment function $h:\mathbb{R}^d\times \mathbb{R}^d\rightarrow \text{Aff}(\mathbb{R}^2$), predicting the affine transformation that best aligns two strokes given their encoded representations. With $h$, we compute a transformation matrix $T^{p}_{s}$ as $T^{p}_{s} = h(z_p, z_s)$ where $z_y = f(y)$ is the feature vector of the encoded sketch/primitive $y$, and $T^{p}_{s}$ the transformation aligning the primitive $p$ to the stroke $s$.

This enables us to compare human strokes with transformed primitive in the next step to create a loss function that minimizes the visual difference. Given a stroke ${s}$, which is represented as a sequence of $m(s)$ connected points, i.e. $s=\{x_1,\dots, x_m\}$ and given a coordinate $g\in G$, with $G$ being a sampled coordinate grid, we can define the influence of the stroke at $g$ as $d(g,{s}) = \max_{i \in \{1,\dots,m(s)-1\},\ r\in[0,1]} \exp \big(-\gamma \; \lvert\lvert g-r\, x_i-(1-r)x_{i+1} \rvert\rvert^2 \big)$. Computing $d(g,s)$ for every coordinate in $G$ we obtain a distance map, also called distance transform where $\gamma$ acts as a smoothing factor. Considering a stroke $s$ and a primitive $p$, we can then define the distance transform loss as $\mathcal{L}_{\text{d}}(s, p{|h}) = \sum_{g\in G} \lvert\lvert d(g,s)- d(g,p{T^{p}_{s})}\rvert\rvert$. With this equation, we are defining a reconstruction loss that sidesteps possible mismatches in the number of points contained in $s$ and $p$ as well as the need of matching points across the two strokes.

With a loss that matches transformed primitives to human strokes, we now need a way to select the best fitting primitive to replace the stroke with. To solve this problem, we inject the compatibility between a stroke and a primitive in the loss function. With this aim, we modify the stroke encoder as $f:\mathcal{S}\rightarrow \mathbb{R}^{2d}$ and, given an input $y$, we divide its embedding into two d-dimensional parts $z_y = [z_y^h, z_y^\phi] = f(s)$, where $z_y^h$ will be the part used to compute the alignment function through $h$ and $z_y^\phi$ will be used to compute the similarity between strokes/primitives. Given this embedding function, we calculate the relative similarity between a target stroke $s$ and a primitive $p$ as $\phi(s,p) = \frac{\exp({\bar z_s^{\phi\intercal}} \bar z_p^\phi / \kappa)}{\sum_{q\in \mathcal{P}}\exp{({\bar z_s^{\phi\intercal}} \bar z_{q}^\phi} / \kappa)}$ where $\kappa$ is a temperature value, and $\bar{z}^\phi_y$ is the L2-normalized version of $z_y^\phi$. Note that while $\phi$ needs to be invariant to the particular poses of $s$ and $p$ to score their compatibility, $h$ in Eq.~(\ref{eq:predicting-transformations}) needs to capture their pose to better align them. These conflicting objectives are what lead us to split the output of $f$ in two parts. With the compatibility scores, we can define our final loss as $\mathcal{L}(s, \mathcal{P}|h,f) = \sum_{p \in \mathcal{P}} \phi(s,p) \; \mathcal{L}_{\text{d}}(s, p T^{p}_{s})$. Notably, the lowest value of $\mathcal{L}(s, \mathcal{P}|h,f)$ is achieved when i) the transformation matrices computed through $h$ align all primitives to the target stroke in the best way (w.r.t. the distance transforms), and ii) the primitives with the highest compatibility scores are the ones that better match the target stroke. Thus, minimizing $\mathcal{L}(s, \mathcal{P}|h,f)$ forces $h$ to output correct transformation matrices and $f$ to encode similar strokes close in the second half of the embedding space, fulfilling both our goals. We name the full model composed of $f$, $h$ and $\phi$ our Primitive Matching Network (PMN).

Sketch Reconstructions

With our PMN model we can now reconstruct human sketches with a small set of predefined primitives. We select the following set of 7 primitives for the reconstructions.

When applying PMN on human sketches, we obtain accurate reconstructions maintaining the semantic structure and class identity of the original sketch.

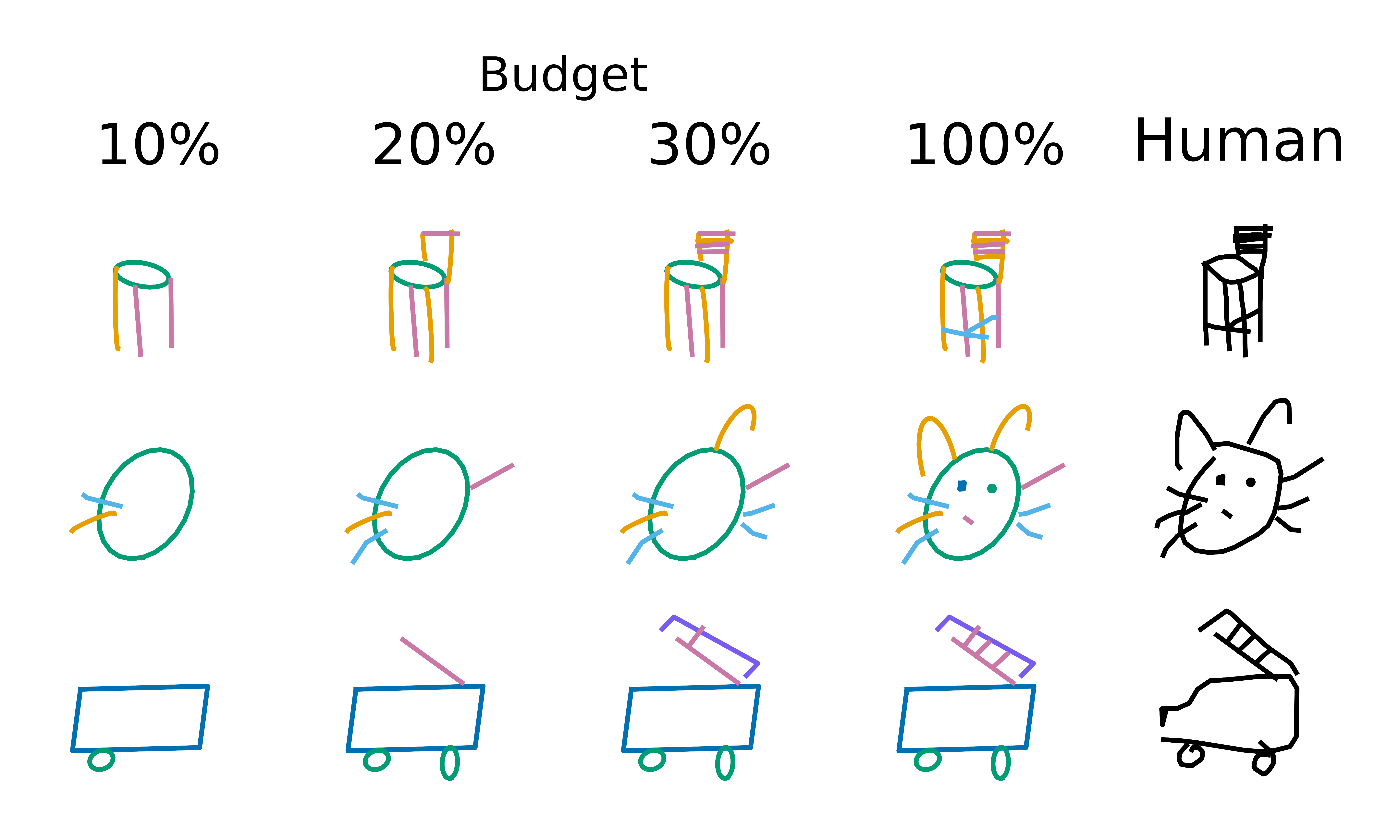
By constructing the sketch from primitive shapes step by step we can be further abstract the sketch and more efficiently communicate the sketch due to the compression achieved by replacing complex strokes with simple primitives.

Zooming out, we can also use our PMN model to get a better understanding of the sketch dataset. For instance, when we train PMN on the Quickdraw dataset, we can extract representative sketches for each class and which primitives are most commonly used when reconstructing sketches of each class.

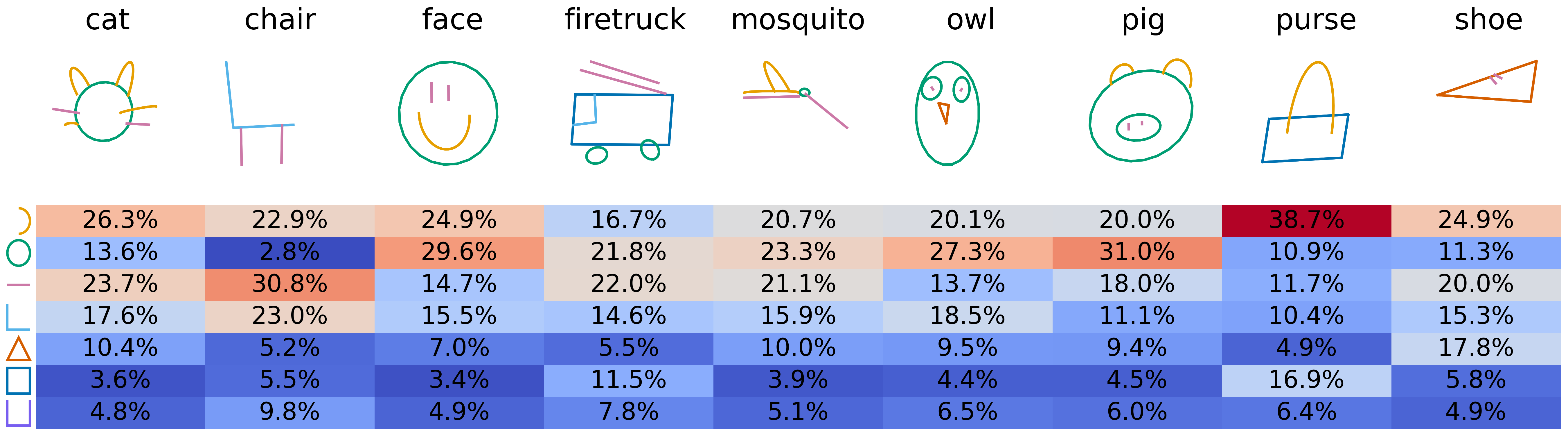
In the table above, we observe that common use cases for arcs include the ears in animals, smiles in faces and handles in purses. Circles most frequently represent heads in animals and faces and firetrucks' wheels. The body of the firetruck and the purse are often represented by rectangles. When comparing the average distribution of primitives per class, we also observe more frequent use of line and corner in chairs or rectangle and arc in purses than in other classes.

Check out the full paper for the complete set of experiments including our qualitative results showing that the PMN abstraction achieves the highest performance given a communication budget (i.e. number of bytes necessary to communicate the sketch) on sketch recognition and fine-grained sketch-based image retrieval tasks.